Wieferich@Home

 

Další @home projekt, tentokrát český a matematický

Přes stále rychlejší počítače není výjimkou, že na některé vědecké problémy jsou stále pomalé. Díky internetu může ale pomoci každý z nás.

Řadu úloh je totiž možné a vhodné řešit distribucí výpočtů na počítače laiků, kteří si na ně jen stáhnou příslušnou aplikaci. Mezi typické úlohy řešené tímto způsobem patří analýza velkého množství statistických dat, zpětné inženýrství DNA, modelování struktury proteinů nebo zkoumání vesmírného vlnění na přítomnost rádiového signálu mimozemšťanů, což je úkolem zřejmě nejznámějšího projektu SETI@home provozovaného Kalifornskou univerzitou v Berkeley od roku 1999.

Právě nyní se rozbíhá nový projekt Wieferich@home, který je z naší české dílny a vznikal na Západomoravské vysoké škole v Třebíči a Vysokém učení technickém v Brně. Jeho úkolem je najít třetí tzv. Wieferichovo prvočíslo, která mají řadu pozoruhodných vlastností a poprvé byla zkoumána německým matematikem Arthurem J. A. Wieferichem (1884-1954) v souvislosti se slavnou Fermatovou větou. Přestože ta je dnes již dokázána, ukazuje se, že význam Wieferichových prvočísel je mnohem větší, mimo jiné jsou známy aplikace v asymetrických kryptografických systémech. Přitom známa jsou dosud pouhá dvě Wieferichova prvočísla: 1093 (objevil W. Meissner v roce 1913) a 3511 (N. G. W. H. Beeger v roce 1922). Není ani známo, zda Wieferichových čísel je nutně konečně mnoho. Dostupná časopisecká literatura uvádí, že zhruba do řádu 10 na 15 (biliarda) neexistuje další Wieferichovo prvočíslo kromě zmíněných dvou; horní hranice se pochopitelně s nasazením výpočetní techniky bude dále posouvat, což je i úkolem projektu Wieferich@home.

Webové stránky projektu jsou http://www.elmath.org. Nainstalováním aplikace nebrzdíte chod svého počítače ani nejste nijak omezeni ve své práci. V době, kdy by počítač byl jinak nečinný, vám ale nyní bude testovat prvočísla z přiděleného intervalu, zda jsou Wieferichova. Můžete si přitom i zajímavě zasoutěžit: ať už jako jednotlivci nebo vytvářením týmů. Možná právě váš výpočet bude pro vědu podstatný.

Obsáhlejší a mnohem podrobnější popis, co jsou to Wieferichova prvočísla naleznete v tohoto článku od Miroslava Kureše.

Na co se to případně nalezené třetí Wieferichovo prvočíslo využije a jaký má tedy význam jej hledat?

Na tuhle otázku odpovídá sám Miroslav Kureš takto:

Tak především: otázka případného nalezení třetího W.p. už je značně prestižní záležitost, kterou se zabývá několik světových pracovišť – má to tedy smysl jen samo o sobě. Ale s touto odpovědí se spokojí málokdo.

Je poměrně zvláštní, že po číslech 1093 a 3511 se velmi dlouho žádné další W.p. nenašlo. Přitom některé pravděpodobnostní argumenty říkají: už je na spadnutí. (Totiž: podle některých z nich v již prozkoumané oblasti mají být více než dvě W.p.) Ale jsou i tací, kdo tvrdí, že další W.p. už neexistuje. Otázka je zajímavá jak z pohledu teorie čísel, tak snad i z hlediska poněkud hlubšího, pokud jde o (ne-)porozumění struktuře nekonečné množiny přirozených čísel.

Není to tak dlouho, kdy prvočísla jako taková neměla výrazné praktické uplatnění, přitom jsou studována od antických dob. Dnes je tomu jinak, díky matematickým metodám pro utajování zpráv. V příspěvku http://www.elmath.org/index.php?id=display_topic&topic=2 píšu o souvislostech W.p. s Mersennovými čísly. Tato čísla jsou používána v kryptografii, a to jak v nejznámějším asymetrickém systému RSA http://cs.wikipedia.org/wiki/RSA, tak i v ECC http://en.wikipedia.org/wiki/Elliptic_curve_cryptography důvodem je jak jejich jednoduchá binární reprezentace, tak fakt, že jsou často prvočísly. Naše skupina se nejvíc zajímá o souvislosti s kryptografií založené na eliptických křivkách, doporučuji např. články:

http://ece.wpi.edu/~sunar/preprints/jrnl_paper.pdf
http://crypt.kaist.ac.kr/papers/JWISC00_CLH.pdf

Tomu jsme se podrobněji do jisté míry věnovali (a budeme věnovat) na našem semináři http://www.math.fme.vutbr.cz/default.aspx?section=113&server=1&article=612.

(Není to ale natolik jednoduché, aby to šlo vyložit zde na omezeném prostoru. Patrně však problém nestojí v tuto chvíli tak, že po případném objevu třetího W.p. dojde v kryptografii k okamžitým revolučním změnám.)

Popis instalace klienta, registrace a přihlášení k týmu

V prvé řadě si z těchto stránek stáhněte klienta projektu. Po stažení instalaci spusťte a dále pokračujte dle popisu:

Všeobecné informace o programu a verzi, kterou se chystáte nainstalovat.

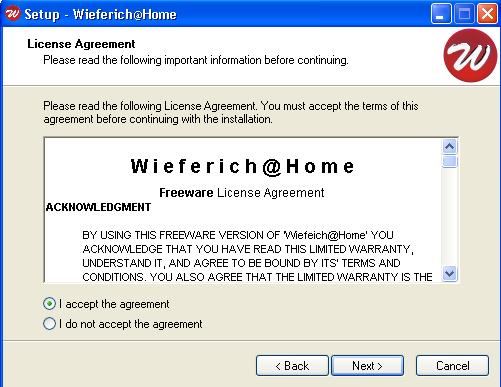
Licenční podmínky. Pro pokračování v instalaci je třeba s nimi souhlasit.

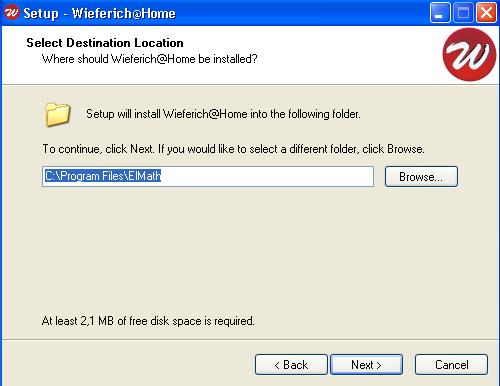
Zvolte cestu, kam se má klient nainstalovat.

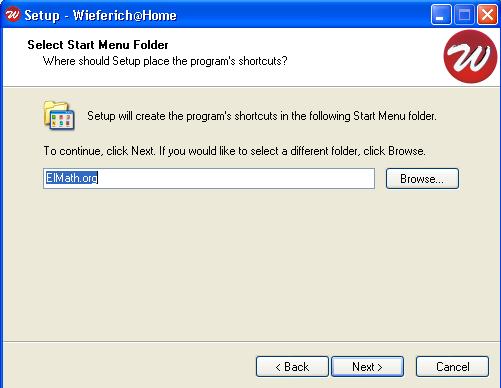
Jméno složky ve Windows.

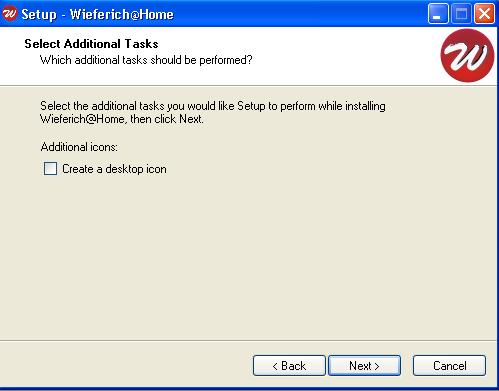
Volba zda se má na ploše vytvořit ikona projektu.

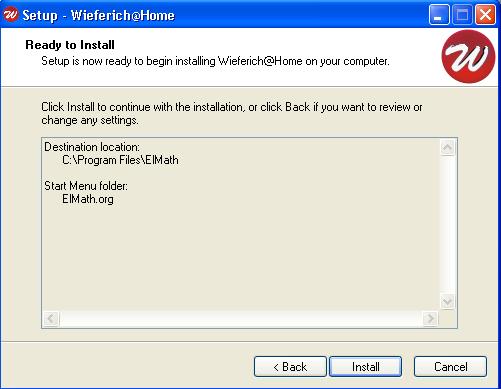
Souhrn všech provedených úkonů, který je třeba potvrdit.

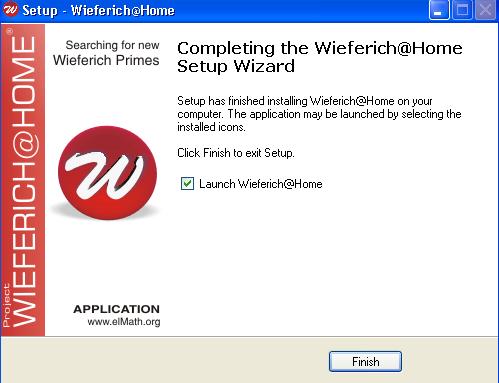
Po instalaci se ukáže toto okno, kde je automaticky zaškrtnutá volba na spuštění klienta.

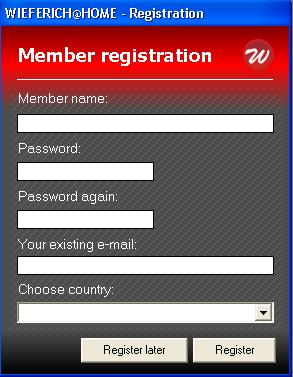
Ihned po spuštění se vám zobrazí registrační formulář. Je potřeba vyplnit všechny kolonky. Pokud již účet máte vytvořený, je potřeba zadat stejné údaje, aby všechny vaše počítače byly pod jedním účtem.

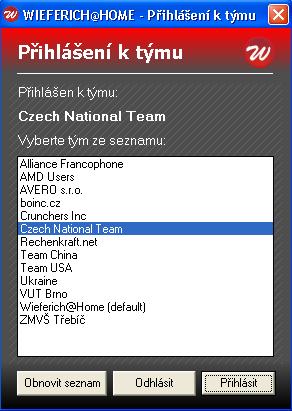
Další volbou je výběr týmu. Tato volba není nutností, ale proč nevstoupit do některého z týmů, když tím můžete podpořit jejich soutěžení, nebo činnost na kterou se zaměřuje.

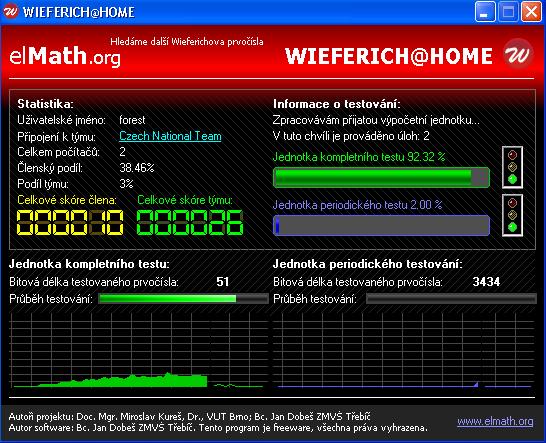
Takto vypadá vlastní průběh výpočtů. Zpracovávají se zároveň 2 prvočísla, každé s jinou náročností. Po dopočítání kteréhokoliv z nich, se automaticky stáhne další a výpočet pokračuje.

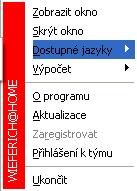
Na závěr ukázka toho, jak vypadá základní ovládací panýlek v systémové liště. Zobrazí se při kliknutí pravým tlačítkem myši na ikonku klienta.

Na závěr malé upozornění. Pokud chcete klienta jen schovat po jeho otevření zpět na lištu, tak přes ovládací panýlek klikněte na volbu "Skrýt okno". Křížkem v rohu totiž klienta ukončíte a tím i výpočty

Autoři článku:
Bc. Jan Dobeš, autor softwaru
Doc. Mgr. Miroslav Kureš, Dr., matematik (Vysoké učení technické v Brně)
Článek doplnil o popis klienta a fotky forest.

Svůj komentář na tento článek, co by mělo být opraveno, či doplněno můžete napsat do této sekce na našem týmovém fóru. Téma s komentářem k tomuto konkrétnímu článku, by mělo nést stejný název, jako článek na webu.