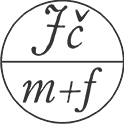-
Prvočíselný rozklad = faktorizace
Prvočíselný rozklad je pojem používaný v matematice, konkrétně v oboru aritmetiky. Jedná se o vyjádření přirozeného čísla ve formě součinu mocnin prvočísel.
DEFINICE
Přirozené číslo "x" je větší než 1. Za jeho prvočíselný rozklad označíme zápis:
Tento zápis musí splňovat následující podmínky:
jsou kladná celá čísla
-
jsou vzájemně různá prvočísla seřazená podle velikosti
PŘÍKLADY
- 2 = 2
- 3 = 3
- 4 = 22
- 6 = 2 ∙ 3
- 8 = 23
- 12 = 22 ∙ 3
- 15 = 3 ∙ 5
-
Základní věta aritmetiky
„Každé přirozené číslo větší než 1 lze jednoznačně rozložit na součin prvočísel.“
To znamená, že prvočíselný rozklad existuje pro každé přirozené číslo větší než 1 a žádné nelze takto rozložit na prvočíslo více způsoby.
-
Faktorizace hrubou silou
S malými čísly lze postupně zvolené číslo zkoušet rozkládat/dělit všemi prvočísly, která jsou menší než rozkládané číslo. Tento algoritmus je jednoduše pochopitelný a implementovatelný. Výpočetní náročnost tohoto algoritmu je ale lineární (náročnost násobně narůstá s velikostí čísla), a pro větší čísla proto nepoužitelný.
PŘÍKLADY
a) 1800 = 23 ∙ 32 ∙ 52
Postup:
1800 : 2 = 900, 900 : 2 = 450, 450 : 2 = 225, 225 : 5 = 45, 45 : 5 = 9, 9 : 3 = 3, 3 : 3 = 1
1800 = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3 ∙ 5 ∙ 5
1800 = 23 ∙ 32 ∙ 52
b) 2800 = 24 ∙ 52 ∙ 7
Postup:
2800 : 2 = 1400, 1400 : 2 = 700, 700 : 2 = 350, 350 : 2 = 175, 175 : 5 = 35, 35 : 5 = 7, 7 : 7 = 1
2800 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 5 ∙ 5 ∙ 7
2800 = 24 ∙ 52 ∙ 7
-
Nejmenší společný násobek
Pomocí prvočíselného rozkladu můžeme snadno určit nejmenší společný násobek dvou čísel. K určení nejmenšího společného násobku vezmeme všechna prvočísla, která se vyskytují minimálně v jednom rozkladu. U každého z nich se použije největší z mocnin, ve které se vyskytuje. Výsledek = prvočíselný rozklad nejmenšího společného násobku.
Pro jednoduchou ukázku využijeme výše uvedené dva příklady faktorizace čísel 1800 a 2800.
Postup:
1800 = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3 ∙ 5 ∙ 5
2800 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 5 ∙ 5 ∙ 7
= 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3 ∙ 5 ∙ 5 ∙ 7
= 24 ∙ 32 ∙ 52 ∙ 7 = 25200
-
Největší společný dělitel
K určení největšího společného dělitele vezmeme všechna prvočísla vyskytující se v obou prvočíselných rozkladech a použijeme u nich pouze nejmenší z mocnin, ve které se vyskytuje. Pokud žádné takové prvočíslo není, největším společným dělitelem těchto čísel je 1.
Tato metoda se nazývá Euklidův algoritmus. V praxi je pro větší čísla nepoužitelný, ale používá se v mnoha algoritmech pro faktorizaci velkých čísel.
Výsledek = prvočíselný rozklad největšího společného dělitele.
Postup:
1800 = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3 ∙ 5 ∙ 5
2800 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 5 ∙ 5 ∙ 7
= 2 ∙ 2 ∙ 2 ∙ 5 ∙ 5
= 23 ∙ 52 = 200
-
Kryptologie
Jedná se o vědu z oboru matematiky, zabývající se utajeným obsahem zpráv, tedy šiframi. Tato věda se dělí dále na kryptografii a kryptoanalýzu.
-
Kryptografie
Zabývá se konstrukcí šifrovacích klíčů, tedy nástrojů napomáhajících k šifrování zpráv. Tato matematická metoda zajišťuje důvěrnost obsahu zprávy, jejího původu, autentizaci (ověření pisatele), integritu (neporušenost). Dále hodnotí rizika dané metody a odolnost vůči útokům (snahám o prolomení). Navrhuje nejrůznější šifrovací systémy, které dokáží převést informaci či zprávu do podoby, v níž je její originální podoba naprosto skryta. Jejím hlavním cílem je udržet obsah zprávy skrytý i v situacích, kdy jí zachytí nepovolaná osoba.
-
Kryptoanalýza
Zkoumá vlastnosti šifrovaného textu a metodu jeho ukryti. Zkoumá kryptografické systémy a napomáhá proniknout jejich zabezpečením k obsahu zprávy.
Úkolem je získat ze zašifrované zprávy otevřený srozumitelný text.
-
Symetrická kryptografie
Základem symetrické kryptografie (neboli šifrování) je použití stejného klíče k šifrování i dešifrování zprávy. Nemělo by být možné bez znalosti klíče převést šifrový text na původní.
VÝHODY
Největší výhodou tohoto šifrování je rychlá a snadná hardwarová i softwarová implementace. Oproti asymetrickému šifrování můžeme pomocí symetrických šifer zašifrovat velké množství dat ve velice krátkém čase a s minimálními nároky na výkon systému. Jednoduché symetrické šifry se také dají kombinovat a dají se tak vytvořit šifry mnohem silnější.
NEVÝHODY
Největší nevýhodou symetrických šifrovacích systémů je, že si obě strany mezi sebou musí vyměnit šifrovací klíč. Také může dojít snadno k jeho vyzrazení a útočníkovi se naskytne příležitost k tomu, aby snadno prolomil jinak silný algoritmus zašifrování každé zprávy. Proto je nutné, aby byly klíče dostatečně často obměňovány.
DVA TYPY SYMETRICKÝCH ŠIFER
Blokové
Jsou hlavním a nejpoužívanějším typem symetrických šifer. Zpracovávají otevřený text předem určené velikosti do šifrovaného textu stejné velikosti. Tento proces musí být reverzibilní = musí být možné provést ten samý proces i v opačném pořadí.
Proudové
Na rozdíl od blokových šifer transformují text v řadě po jednotlivých bitech. Znaky se šifrují postupně a odděleně. Jsou užitečné v prostředí, kde dochází k velkým ztrátám při přenosu. Jsou méně náročné než blokové šifry, a lze je tedy využít i v systémech s menším výkonem.
PŘÍKLAD SYMETRICKÉ ŠIFRY
CAESAROVA ŠIFRA
- Klíč = číslo "n" je jakékoli číslo od 1 do 25
- Šifrování – každé písmeno se posune o "n" pozic v abecedě dopředu
- Dešifrování – každé písmeno se posune o "n" pozic v abecedě dozadu
- Klíč = n = 5
- Původní zpráva = ahoj
- Šifrovaná zpráva = fmto
- Tato šifra není příliš bezpečná – jen 25 možných klíčů
-
Asymetrická kryptografie
Asymetrická kryptografie neboli kryptografie s veřejným klíčem je skupina kryptografických metod, které pro šifrování a dešifrování používají odlišné klíče. To je základní rozdíl oproti symetrické kryptografii. Ta používá k šifrování i dešifrování jediný klíč.
Od poloviny 70. let 20. století umožnila asymetrická kryptografie zajistit nejen důvěrnost (znemožnit čtení nepovolané osobě), ale také zajistit identifikaci autora zprávy pomocí veřejného klíče a nepopiratelnost zprávy (zprávu mohl vytvořit jen vlastník privátního klíče).
PŘÍKLAD ASYMETRICKÉ ŠIFRY
- Alice má svůj privátní klíč a Bob zase svůj.
- Alice chce svoji zprávu poslat Bobovi, a tak ji zašifruje Bobovým veřejným klíčem.
- Bob pak zprávu rozšifruje.
- Poté chce Bob poslat zprávu Alici, a tak ji zašifruje jejím veřejným klíčem.
ZÁKLADNÍ PRINCIPY
Klíč pro šifrování v asymetrické kryptografii sestává ze dvou částí: první část se používá pro šifrování zpráv, druhá část se používá pro dešifrování. Ten, kdo šifruje, tedy nemusí s dešifrujícím příjemcem zprávy sdílet nic tajného, čímž eliminují potřebu výměny klíčů. To je hlavní výhoda asymetrické kryptografie.
Běžně se v asymetrické kryptografii využívá tzv. veřejný a soukromý klíč. Šifrovací klíč je veřejný, majitel klíče ho volně uveřejní, a kdokoli jím může šifrovat jemu určené zprávy. Klíč k dešifrování je privátní (soukromý), majitel jej drží v tajnosti . Pomocí něj může tyto zprávy dešifrovat.
Šifrovací klíč "e" a dešifrovací klíč "d" jsou spolu matematicky svázány. Nezbytnou podmínkou pro šifru je praktická nemožnost ze znalosti šifrovacího klíče spočítat dešifrovací.
Asymetrická kryptografie tedy matematicky postupuje tímto způsobem:
Šifrování: c = f(m, e)
Dešifrování: m = g(c, d)
kde "m" je zpráva, "c" zašifrovaná zpráva, "e" šifrovací klíč, "d" dešifrovací klíč, šifrovací funkce "f", dešifrovací funkce "g"
Šifrovací a dešifrovací funkce se mohou lišit. Přinejmenším jsou si ale velmi podobné.
MECHANISMY FUNKCE
Asymetrická kryptografie je založena na tzv. jednocestných funkcích. Jsou to operace, které lze snadno provést pouze v jednom směru – ze vstupu lze snadno spočítat výstup, z výstupu je však velmi obtížné nalézt vstup. Nejsnadněji můžeme tuto metodu přirovnat k násobení – je velmi snadné vynásobit dvě i velmi velká čísla. Rozklad součinu na činitele (faktorizace) je však velmi obtížný. Při použití více čísel již prakticky nemožný.
SLABINY
Je zde možnost, že by dané osobě někdo mohl odhalit/dešifrovat ze zachycené zprávy privátní klíč. V praxi se lze často tomuto riziku vyhnout volbou dostatečně dlouhého klíče. Vyskytuje se zde i možnost prolomení šifry pomocí kvantového počítače. Proto se aktuálně pozornost obrací k algoritmům s matematicky dokázanou bezpečností. Jsou to takové algoritmy, které neprolomí ani kvantový počítač. Říkáme jim post – quantum cryptography.
Bezpečnost musí být zvážena kromě odolnosti proti útoku konkrétní dvojice klíčů i při rozmisťování systémů veřejných klíčů. U několika dříve slibných asymetrických klíčových algoritmů byly odhaleny určité slabiny, a tak tyto algoritmy již nejsou považovány za tak bezpečné jako dříve. Jedním ze způsobů, jak předejít útokům, je použití certifikační autority. Tento způsob poskytuje uživatelům digitální certifikát odolný proti násilnému otevření. Takové certifikáty jsou podepsány datovými bloky, takže veřejný klíč patří určité společnosti, osobě, nebo jinému subjektu. I tento přístup má své slabiny. Musíme věřit, že autorita vydávající certifikát správně zkontrolovala identitu držitele klíče a že zajistila správnost veřejného klíče v době vydání.
VÝPOČETNÍ NÁROČNOST
Algoritmy pro asymetrické šifrování jsou oproti symetrickým algoritmům podobné úrovně bezpečnosti výrazně náročnější. Hlavním rozdílem je užívání podstatně delších klíčů.